définissable

définissable

définissable [ definisabl ] adj.
• fin XVIIe; de définir
♦ Que l'on peut définir. Sentiment difficilement définissable. Primitif non définissable. ⊗ CONTR. Indéfinissable.

● définissable adjectif Qui peut être défini. ● définissable (synonymes) adjectif Qui peut être défini.
Contraires :
- indéfinissable

définissable
adj. Que l'on peut définir.

⇒DÉFINISSABLE, adj.
[En parlant d'un inanimé surtout abstr.] Qui peut être défini. Anton. indéfinissable. Des sentiments mal définis et peu définissables (LEMAITRE, Contemp., 1885, p. 147). Les nombres définissables (...) infiniment plus rares que les nombres non définissables (E. BOREL, Paradoxes infini, 1946, p. 181) :
• Quand nous parlons, dans ce qui précède, de termes impossibles à définir, nous n'avons point en vue les définitions telles que les entendent les lexicographes et les logiciens (...). Les mots « nombre, angle » ne sont pas définissables, suivant la notion que l'on a communément de la définition; et pourtant les idées correspondantes sont rigoureusement définies ou déterminées...
COURNOT, Essai sur les fondements de nos connaissances, 1851, p. 332.
Prononc. et Orth. :[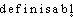]. Ds Ac. 1878 et 1932. Étymol. et Hist. [Début XVIIIe s., S. Simon d'apr. FEW t. 3, p. 30 a]; 1740 (CASTEL, L'Optique des couleurs, p. 127). Dér. du rad. de définisseur; suff. -able. Fréq. abs. littér. :54.

définissable [definisabl] adj.
ÉTYM. Fin XVIIe; de définir.
❖
♦ Que l'on peut définir. || Les mots « primitifs » ne sont pas définissables. || Éprouver un sentiment très définissable.
❖
CONTR. Indéfinissable.

Encyclopédie Universelle. 2012.

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • DÉFINISSABLE — adj. des deux genres Que l’on peut définir. Il y a dans toutes les langues des mots qui ne sont pas définissables …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • définissable — (dé fi ni sa bl ) adj. Que l on peut définir. ÉTYMOLOGIE    Définir …   Dictionnaire de la Langue Française d'Émile Littré

  • Nombre Définissable — Un nombre définissable, nommé aussi parfois nombre accessible[1], ou nombre nommable[2], correspond à la notion intuitive décrite par Emile Borel [3] de « nombre pouvant être décrit comme un objet mathématique, de sorte que ceux qui en… …   Wikipédia en Français

  • Nombre definissable — Nombre définissable Un nombre définissable, nommé aussi parfois nombre accessible[1], ou nombre nommable[2], correspond à la notion intuitive décrite par Emile Borel [3] de « nombre pouvant être décrit comme un objet mathématique, de sorte… …   Wikipédia en Français

  • Nombre définissable — Un nombre définissable, nommé aussi parfois nombre accessible[1], ou nombre nommable[2], correspond à la notion intuitive décrite par Emile Borel [3] de « nombre pouvant être décrit comme un objet mathématique, de sorte que ceux qui en… …   Wikipédia en Français

  • Ensemble définissable — En mathématiques, un ensemble définissable est une relation m aire sur le domaine d une structure dont les éléments sont précisément ceux qui satisfont une formule donnée dans le langage de la structure. Un ensemble E peut être défini avec ou… …   Wikipédia en Français

  • Indéterminabilité — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… …   Wikipédia en Français

  • Theoreme d'incompletude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… …   Wikipédia en Français

  • Théorème d'incomplétude — de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sur les… …   Wikipédia en Français

  • Théorème d'incomplétude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”